Probabilistic Search for Randomly Moving Targets

🕒 Estimated reading time: 8–10 minutes

Overview

This project aims to optimize controls of autonomous agents searching for randomly moving targets (non-evasive and evasive). Computational frameworks are proposed to iteratively confine control strategies, balancing the information gathering and agents mobility. We present three complementary developments: (i) a continuous-discrete observation framework, (ii) a time-periodic search strategy tailored for non-evasive targets, and (iii) a collaborative search approach for tracking evasive targets. An example of probabilistic search, on finding the lost pet, is shown in Figure 1 below.

Figure 1. An illustration of the probabilistic search problem. A drone acts as the searcher, actively observing the environment while moving. The target, a lost pet whose position is unknown to the drone, moves randomly in the field. The searcher's actions adapt based on observations made along its path to infer the target's location.

Keywords: Probabilistic search theory · Stochastic dynamics · PDE-constrained optimization · Adjoint analysis

Motivation

Search problems are common in both military and civilian domains—from rescuing missing persons, pets or wreckage like MH370 (non-evasive randomly moving targets), to tracking fugitives or foraging animals (evasive randomly moving targets). Unfortunately, many traditional methods are limited in adaptability and struggle in uncertain environments. Figure 2a and 2b below showcase the real-world challenges, even just for a stationary target shown in Figure 2a, often resorting to predetermined or exhaustive sweeps.

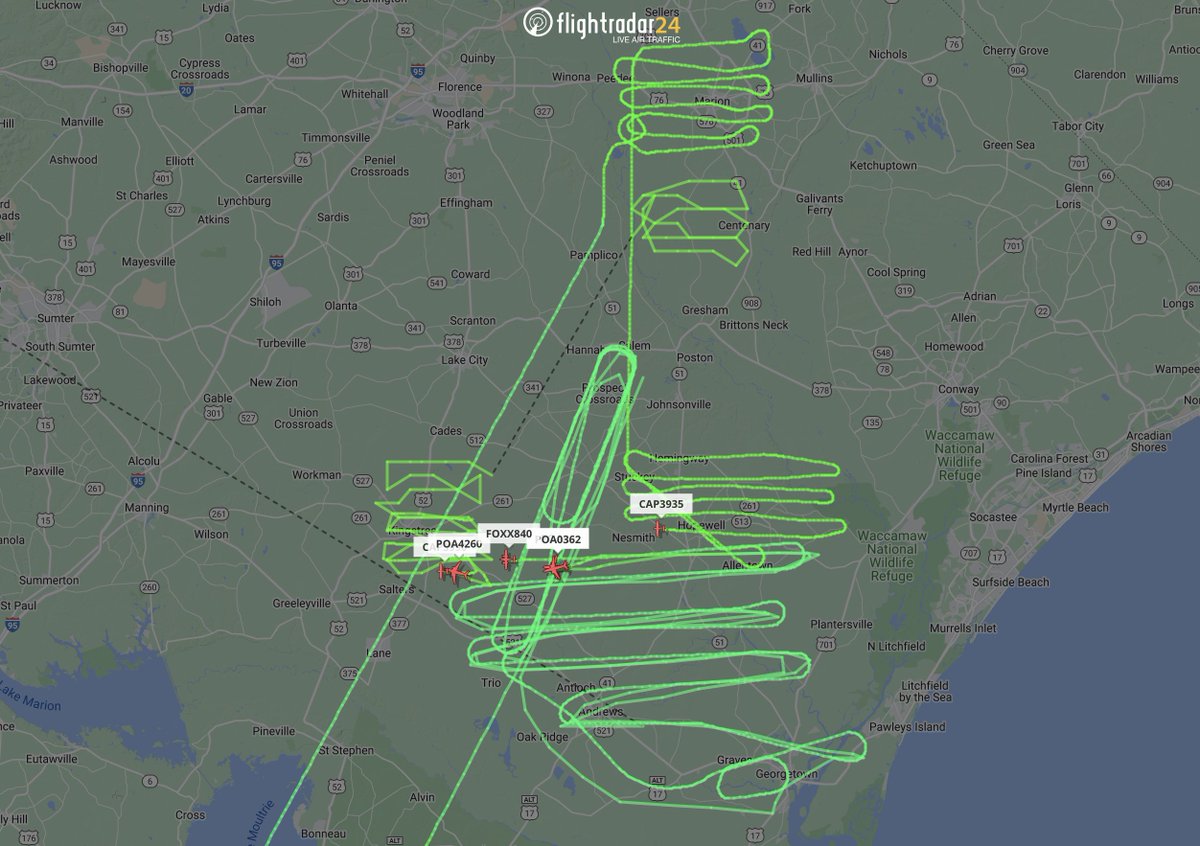
Figure 2a. Lawnmower trajectory used to search for the missing $109M F-35B fighter jet in 2023. Image source

Figure 2b. Searching for the debris of MH370. Image source

Key challenges in theory

Previous state-of-the-art work in probabilistic search has several limitations:

Phelps et al. [2014] considers only uncertainty in the target’s initial location, neglecting uncertainty in its motion;
Hellman [1970] focuses on optimizing search trajectories, but ignores dynamic feasibility of searchers;
Ohsumi [1991] introduces dynamic programming for optimal control, but is computationally intensive and impractical for complex models;

In contrast, the computational frameworks developed in this project will not only tackle the aforementioned challenges, but will also propose modeling for non-evasive target, or even evasive.

Methodology and Numerical Results

The crux of this project is adaptive observation, a framework that couples estimation and control. The estimation task involves modeling the moving target’s likely position as a stochastic process, accounting for the uncertainty in both its initial location and dynamics. The control task involves decision-making and coordination of searchers as they scan their surroundings to locate the target. Crucially, these two components are organically coupled: searchers’ observations not only inform the evolving estimate of the target’s location, but also respond to it, forming a “feedback loop” that iteratively drives both estimation and control tasks. This idea is illustrated in Figure 3 below.

Figure 3. Schematic of the search process in discrete time. The red lines highlights the core feedback loop: searchers’ observations inform the estimate (i.e., the probability density function of the target), which in turn updates searchers' controls (and consequently, the trajectories). This project developed the result in continuous-time, while the diagram is shown in discrete-time for illustration purposes only.

In this homepage, we focus on showcasing numerical results. For detailed mathematical background—including the modeling of the target’s motion via stochastic differential equations, the evolution of the target’s probability density function (PDF) using Fokker-Planck equation, and the formulation of the optimal control problem—please click the blue section titles below for more details.

Part 1 Continuous-discrete observation

We first consider a hybrid search framework in which the target’s motion evolves continuously in time, while observations are made at discrete time steps. The core challenge lies in optimizing searcher controls under uncertainty while accounting for the evolving probability density function (PDF) of the target’s position.

Figure 4. Real-time animation of two autonomous searchers performing hybrid search. The searcher trajectories are shown in blue and orange, with planned trajectories in lighter dotted lines in the horizon. The grayscale background illustrates the evolving probability density function (PDF) of the target’s location: darker regions (close to searchers) indicate lower probability (suppressed by searchers' observation), while lighter regions (far from searchers) represent areas of higher uncertainty and likelihood of target presence. The adaptive control strategy drives the searchers to iteratively explore and shape the PDF landscape (exploring lighter regions) in pursuit of the hidden target.

Figure 5. Time evolution of control inputs for the two autonomous searchers. The top and bottom panels correspond to Agent 1 and Agent 2, respectively. Solid curves represent the executed control inputs $\mathrm{u}_1$, $\mathrm{u}_2$ applied over time, while the lighter dashed lines indicate the planned control trajectories within each predictive horizon. These results illustrate how hybrid search dynamically adjusts control strategies in response to updated PDF of target position.

Part 2 Optimized periodic orbits

Inspired by the periodic-like trajectories obtained from optimizing hybrid search strategy as shown in Figure 4 above, Zhao and Bewley [2025] investigates a periodic search strategy for randomly moving targets. By optimizing the controls—and thus periodic trajectories—of multiple autonomous agents, the approach efficiently shapes the long-term probability landscape to maximize detection rate under uncertainty.

Figure 6. Results of optimized periodic search strategy with three autonomous agents. Top-left: optimized periodic trajectories of the searchers in blue, orange, and yellow. Top-right: convergence of the objective functional, and periodic constraint over iterations, indicating successful adjoint-based optimization. Bottom-left: optimized control inputs $u_1$ and $u_2$ for each agent across one period. Bottom-right: validation of time-periodicity using the trajectory mismatch metric $\gamma(t)$, along with its time-averaged integral. The dashed traces represent previous iterations, and the red horizontal line marks the convergence target. These results demonstrate the effectiveness of time-periodic orbit design for persistent probabilistic search.

Figure 7. Three autonomous searchers executing periodic search trajectories, shown in blue, orange, and yellow. The grayscale background depicts the evolving probability density function (PDF) of the target’s location: darker regions near searchers represent suppressed likelihood due to the search effect, while lighter regions indicate higher probability areas where the target is more likely to reside. The coordinated periodic motion helps maintain spatial coverage and adaptively sculpts the uncertainty landscape over time.

Part 3 Collaborative search strategy

Under construction

Part 4 Probabilistic search for grid-based Bayesian estimation exploiting sparsity

Theory and code under development…

Conclusion

We presents principled frameworks for optimizing controls of autonomous agents searching for randomly movingtargets. This project concludes:

The proposed framework can efficiently locate the unseen target even under mobile uncertainty;
There is enough control authority for optimizing searchers controls (and thus, trajectories), and the proposed adjoint analysis can guide the control synthetics;
The proposed periodic and collaborative search strategy can efficiently find the evasive target, balancing the spatial coverage with control efficiency.

Numerical results demonstrate fast convergence of the objective and control inputs, as well as successful periodicity enforcement via adjoint-based gradient optimization. This approach is particularly well-suited for long-duration, passive monitoring tasks such as rescue-and-save missions, persistent surveillance, and environmental monitoring.

References

Chris Phelps, Qi Gong, Johannes O. Royset, Claire Walton, and Isaac Kaminer. Consistent approximation of a nonlinear optimal control problem with uncertain parameters . Automatica, 50(12):2987–2997, 2014.
Olavi Hellman. On the effect of a search upon the probability distribution of a target whose motion is a diffusion process . The Annals of Mathematical Statistics 41.5 (1970): 1717-1724.
Akira Ohsumi. Optimal search for a Markovian target . Naval Research Logistics (NRL), 38(4):531–554, 1991.
Muhan Zhao and Thomas R. Bewley, Probabilistic search for randomly moving targets using optimized time-periodic orbits, under review at Automatica since Feb. 2025.